Music and Acoustics
Lecture I: Pitch
Pythagoras
What is the wisest thing? Number. What is the most beautiful? Harmony.
—Pythagorean dogma (in Taylor, Iamblichus' Life of Pythagoras, 43)
Questions
- What musical parameters or dimensions are measurable? What instruments do we use to measure them?
- Is music an art or a science?
- Does beauty exist for a reason? (Is beauty a manifestation of order?)
- What is harmony?
Introduction: dissertation work
- Harmony as a threefold relation between music, mathematics, and community
- Points of interest: the ancient Greeks; Renaissance Italy; Enlightenment France and Germany
Once upon a time, a philosopher invented harmony by confusing the beautiful with the wise. One day, he was walking through the streets of his village, dreaming of measurement. He already knew how to measure the objects of sight and touch: he could compare distances with a ruler and compass, and weights with a balance. Was it possible, he wondered, to measure sounds? Was there another tool, another instrument, that could assist the hearing through the aid of numbers? As he considered this problem, he walked by a blacksmiths' shop, and heard—whether by fortune or desire—consonance. As the blacksmiths struck a piece of iron with their hammers, perfect octaves, fifths, and fourths resounded.
The excited philosopher was not satisfied to listen to these intervals; instead, he wanted to understand why they sounded so beautiful. More precisely: since he already believed that numbers were the source of everything beautiful, he wanted to find a mathematical principle to explain the intervals’ consonance. So he interrupted the blacksmiths’ work, borrowed all their hammers, and started to experiment. He hammered on different pieces of metal; he varied the force of his blows. He concluded that the tuning of the hammers had nothing to do with the material he hit, or how hard he hit it. Then he weighed the hammers on his balance. He discovered, to his delight, that a hammer weighing twice as much as another sounded an octave lower than it; that one weighing two-thirds as much sounded a fifth lower; that one weighing three-fourths as much sounded a fourth lower. As he had expected, the beauty of the hammers’ consonances corresponded to the elegant proportions of their weights. Then he went home to build a lyre out of metal weights and wires, using the integer ratios he had just discovered.

Pythagoras playing his lyre. The 4:6:8:9:12:16 weights ideally produce the six-note scale C3-G3-C4-D4-G4-C5 (smaller weights create less tension and therefore lower sounds.)
By building the lyre, the philosopher had realized his dream of an instrument that could measure sounds. He had invented harmony—some would even say music itself. But he was not content to keep his invention a secret. He wanted to share music with his students, to improve their lives and correct their manners with it. The philosopher therefore established a musical community. Before his students went to bed, they sang songs to put their minds at ease. When they woke up, they sang other songs to reanimate themselves. As they went about their day, music moderated their passions and kept them healthy. The community flourished through its faith in harmony—that is, in the correspondence between the wisdom of the integers, the beauty of sounds, and their own unity.
What is wise, however, is not necessarily beautiful. A mathematical principle is no guarantee of harmony: although it may produce consonance, it may also produce discord. And given consonance and discord, two people with two different sets of ears may confuse one for the other; indeed, this is the problem the philosopher was trying to solve in the first place. The community could not confirm that the philosopher was correct to identify the consonance of the hammers as the truly beautiful. It could not know if he chose the right numbers—the integers—as the foundation of their own music and unity. Rather, it could only follow the philosopher's logic just enough to confirm its own harmony, taking care not to reveal any other.
The community simply needed to hear an alternative to their own harmony, to realize that it was no better than anyone else’s. It was only a matter of time before a student discovered a new number—the square root of two—and a new sound—the tritone. The dissonant interval was literally incommensurable with the consonances of fourths, fifths, and octaves, but its mathematical principle was no less reasonable. The student had invented a harmony that was both perfectly intelligible and completely at odds with the philosopher’s. Such a revelation was both impudent and dangerous, and it cost the student his life; he drowned at sea, the victim of mysterious forces. Still, his punishment came too late to preserve the unity of the community. The tritone had already split it in two, by demonstrating that faith in harmony meant two contradictory things. On one hand, it meant submitting to the philosopher’s principle for the sake of the community. On the other, however, it meant following the philosopher’s example to discover a new principle, even at the expense of tearing the community apart.
At the dawn of music history, in the 5th century BC, Pythagoras founded his harmonious sect, and Hippasus was cast into the sea for dividing it. Their legend exposes a fundamental problem of Western musical thought. Although mathematics can generate and describe count musical relationships, it cannot prove which of these are musically valid and which are not. Nevertheless, following the lead of the acusmatici—the Pythagoreans who simply listened and obeyed—most musicians over the last 2500 years have appealed to the authority of a “correct” musical mathematics, the “true” harmony that is both the symbol and practice of their musical community. But a handful of other musicians, playing the role of Hippasus, have called their bluff: insofar as mathematics produces musical authority and community, it also produces its radical alternative, namely the anarchy of the mathematici—the musicians who reason for themselves.
Pythagoras' discovery of a numerical notation system for sounds was as fateful for music as Edison's invention of the phonograph. The discovery established a science of sound, which the ancient Greeks called harmonics, and which is the basis of modern acoustics. More importantly for us, Pythagoras reinterpreted the art of music from the perspective of science; he reframed an aesthetic problem—the problem of musical beauty—as a technological one—the problem of sonic measurement. I cannot overstate either the dubiousness of this reframing or its impact on the history of musical thought. From around 1000 AD to 1800 AD, harmony was the prince of musical concepts, and pitch the king of musical parameters. I have already described how the theorists of plainchant used the Greek sound-science to structure their own notation.
Ptolemy
Quotes: music and reason
Perception needs as its crutch, as it were, the educational assistance of reason.
—Ptolemy (trans. Jon Solomon), Harmonics, Book I. § 3.14 (p. 4)
[T]here is need, as there is for sight, of some rational criterion for [sound and hearing] from the appropriate instruments, just as the straight edge has, so to speak, need of a ruler, and the circle and the measurement of its parts have need of a compass. In the same way, the hearing, which is, along with sight, for the most part a messenger for the theoretical and rational aspect of the soul, needs some reasoned approach, too, for those things its nature cannot judge accurately, which it will not contradict but confirm as correct.
—Ibid., Book I. § 5.2 (p. 6)
For in every subject it is inherent in observation and knowledge to demonstrate that the works of nature have been crafted with some reason and prearranged cause and completed not at all in random or as it happened, particularly in its most beautiful constructions which are simply those of the sense perceptions most closely related to reason—sight and hearing.
—Ibid., Book I. § 5.19 (p. 8)
Tools for the job
We must give up examining our subject by means of auloi and syrinxes or weights attached to strings, for such demonstrations cannot bring us to accurate conclusions.
Instead they invite slander upon their undertakings, for the auloi and syrinxes are difficult to examine, and even if their inconsistencies are corrected, their limits, which are necessary for comparing lengths, are still only vaguely established. In the majority of wind instruments there is in addition generally some irregularity as well in the flow of air. With weights attached to strings, the strings are not kept unchanged in relation to each other. . . .
Similar difficulties occur with sounds produced by percussion, sounds which one sees produced by hammers of unequal weight or disks and by full or empty vessels, for it is indeed a great task to observe in all of these constancy in matter and form.
The string which is stretched across the canon, as it is called, will show us both more accurately and more easily the ratios of the consonances, not, of course, in random tuning, but first with some examination of the irregularity that would occur with the apparatus, and then of the proper placing of the limits of those parts to be played in them, by which the whole length is defined, might have their proper and clear points of origin.
—Ibid., 24–26.
Aristoxenus
In the fourth century BC, Aristoxenus, a pupil of Aristotle, writes The Elements of Harmony, in which he rails at the Pythagoreans for confusing mathematical and musical knowledge. A century-and-a-half earlier, the legendary Pythagoras discovers the ratios of string lengths that produce octaves, fifths, and fourths; these ratios, if you recall, are respectively 2/1, 3/2, and 4/3. Pythagoras' discovery of a numerical notation system for sounds is no less profound than Edison's invention of the phonograph. It establishes a science of sound, which the ancient Greeks call harmonics. To understand sound, Pythagoras argues, is to inscribe the numbers that animate it. Several generations later, however, Aristonexus disagrees with the founder of the harmonic discipline. The problem, he argues, is that numbers are bad musical models because they are too precise:
What the voice cannot produce and the ear cannot discriminate must be excluded from the available and practically possible range of musical sound. In the progress in parvitatem [i.e. in distinguishing smaller and smaller intervals] the voice and the ear seem to fail at the same point. The voice cannot differentiate, nor can the ear discriminate, any interval smaller than the smallest diesis, so as to determine what fraction it is of a diesis or of any other of the known intervals.
Aristoxenus proposes that there is a limit of musical production and perception: a smallest interval that the voice can sing, and that the ear can hear. Anything smaller than that sounds the same. His argument is not simply an appeal to musical practicality, but also an assault on the numerical representation of sounds. Numbers, which are digital and therefore can represent sounds with arbitrarily precision, are too subtle to represent meaningful musical information.
Tuning example: the Pythagorean comma
Aristoxenus' complaint is not an objection to Pythagoras' elegant ratios representing consonances. Ratios such as 2/1, 3/2, and 4/3 please the mind in their simplicity, and represent sounds that are pleasing to the ear. If the Pythagoreans limited their science to octaves, fifths, and fourths, there would be no problem. But numbers can represent not only harmonic consonances, but also thorny and obscure dissonances, which emerge as the gaps between consonance intervals. For example, it is mathematically verifiable that stacking twelve perfect fifths on top of each other produces an interval just barely in excess of seven octaves.
- The ratio for the fifth is 3/2; a fifth above that is 3/2 x 3/2, or 9/4; the fifth above that is
, and so on. The ratio of twelve stacked fifths is therefore
, or
.
- The ratio for the octave is 2/1 (2:1), or just 2. The ratio for seven stacked octaves is
, or 128.
- To find the difference between two intervals, we divide the larger interval ratio by the smaller. For example, to find the difference between the octave and the fifth, we calculate 2 / (3/2) = 4/3: a fourth, as we expect. The difference between twelve perfect fifths and seven octaves, then, is
, or
.
The interval ratio 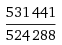 is called a Pythagorean comma. The ease with which one may write the numbers of this minute interval, and identifying it by eye, is incommensurate with the difficulty of producing it on a monochord, or identifying it by ear. It's easy enough to measure the difference between 3/2 and 4/3, but what about the difference between 531441/524228 and 531442/524229?
Aristoxenus argues that such differences, and therefore numbers themselves, are irrelevant to music theory. Rather than putting their faith in headache-inducing calculations, music theorists should listen instead to the wobbly voice, which has a limit to its fine-tuning.
is called a Pythagorean comma. The ease with which one may write the numbers of this minute interval, and identifying it by eye, is incommensurate with the difficulty of producing it on a monochord, or identifying it by ear. It's easy enough to measure the difference between 3/2 and 4/3, but what about the difference between 531441/524228 and 531442/524229?
Aristoxenus argues that such differences, and therefore numbers themselves, are irrelevant to music theory. Rather than putting their faith in headache-inducing calculations, music theorists should listen instead to the wobbly voice, which has a limit to its fine-tuning.